如图，定义：在Rt△ABC中，∠C =90°,锐角α的邻边与对边的比叫做角α的余切，记作ctanα，即ctanα=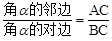
.
根据上述角的余切定义，解答下列问题：
（1）ctan60°= .
（2）求ctan15°的值.
为
上一点，点
分别在
，
，
．求证：
． 
，其中
相关知识点
推荐套卷
如图，定义：在Rt△ABC中，∠C =90°,锐角α的邻边与对边的比叫做角α的余切，记作ctanα，即ctanα=.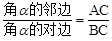
根据上述角的余切定义，解答下列问题：
（1）ctan60°= .
（2）求ctan15°的值.
粤公网安备 44130202000953号