已知△ABC是边长为l的等边三角形,D、E分别是AB、AC边上的点,AD = AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到三棱锥A-BCF,其中 .
.
(1)证明:DE∥平面BCF;
(2)证明:CF⊥平面ABF;
(3)当 时,求三棱锥F-DEG的体积V.
时,求三棱锥F-DEG的体积V.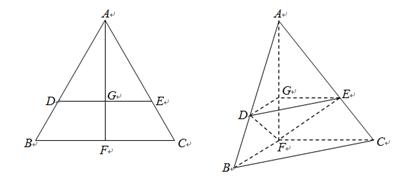
推荐套卷
已知△ABC是边长为l的等边三角形,D、E分别是AB、AC边上的点,AD = AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到三棱锥A-BCF,其中 .
.
(1)证明:DE∥平面BCF;
(2)证明:CF⊥平面ABF;
(3)当 时,求三棱锥F-DEG的体积V.
时,求三棱锥F-DEG的体积V.