某品牌的饼干袋里,装有动物、笑脸、数字三种花纹的饼干(除花纹外其余都相同),其中有动物花纹饼干2个,笑脸花纹饼干1个,数字花纹饼干若干个,现从中任意拿出一个饼干是动物花纹的概率为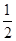 .
.
(1)求口袋中数字饼干的个数;
(2)小亮同学先随机拿出一个饼干吃掉,又随机拿出一个饼干吃掉,请用“树状图法”或“列表法”,求两次吃到的都是动物花纹饼干的概率.
相关知识点
推荐套卷
某品牌的饼干袋里,装有动物、笑脸、数字三种花纹的饼干(除花纹外其余都相同),其中有动物花纹饼干2个,笑脸花纹饼干1个,数字花纹饼干若干个,现从中任意拿出一个饼干是动物花纹的概率为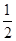 .
.
(1)求口袋中数字饼干的个数;
(2)小亮同学先随机拿出一个饼干吃掉,又随机拿出一个饼干吃掉,请用“树状图法”或“列表法”,求两次吃到的都是动物花纹饼干的概率.