如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;
(3)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
相关知识点
推荐套卷
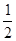 x2+bx-2与x轴交于A、B两点,与y 轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y 轴交于C点,且A(一1,0).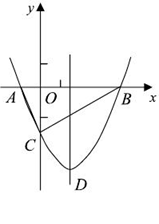

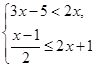
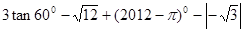
 经过A(3,0),B(0,-3)两点,点P是直线AB上一动点,过点P作
经过A(3,0),B(0,-3)两点,点P是直线AB上一动点,过点P作 轴的垂线交抛物线于点M,设点P的横坐标为t,
轴的垂线交抛物线于点M,设点P的横坐标为t, 的面积。
的面积。
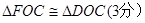
 的值
的值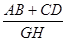 的值
的值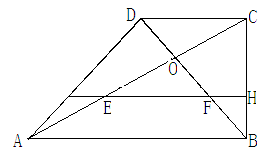
 粤公网安备 44130202000953号
粤公网安备 44130202000953号