已知圆C的方程为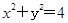
，过点M（2，4）作圆C的两条切线，切点分别为A，B，
直线AB恰好经过椭圆T：
（a＞b＞0）的右顶点和上顶点．
（1）求椭圆T的方程；
（2）已知直线l：y＝kx＋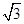
（k＞0）与椭圆T相交于P，Q两点，O为坐标原点，
求△OPQ面积的最大值．
相关试题
中，
且
，求公比q及前6项的和．
中，角A、B、C的对边分别为
，已知向量
且满足
．
试判断
且
∥
．
，求x与y的值及四边形ABCD的面积．
为等差数列，
为数列
项和，已知
，
，
为数列
的前
．相关知识点
推荐套卷
已知圆C的方程为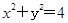，过点M（2，4）作圆C的两条切线，切点分别为A，B，
直线AB恰好经过椭圆T：（a＞b＞0）的右顶点和上顶点．
（1）求椭圆T的方程；
（2）已知直线l：y＝kx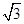＋（k＞0）与椭圆T相交于P，Q两点，O为坐标原点，
求△OPQ面积的最大值．
粤公网安备 44130202000953号