初中生的视力状况受到全社会的广泛关注,某市有关部门对全市3万名初中生视力状况进行了一次抽样调查,如图是利用所得数据绘制的频数分布直方图(长方形的高表示该组人数),根据图中所提供的信息,回答下列问题:
(1)本次调查共抽测了 名学生,占该市初中生总数的百分比是 ;
(2)从左到右五个小组的频率之比是 ;
(3)如果视力在4.9以上(含4.9)均属正常,则全市有 名初中生的视力正常, 视力正常的合格率是 .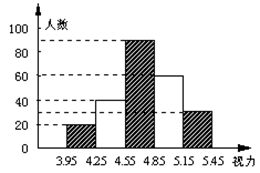
相关知识点
推荐套卷

 过点A。
过点A。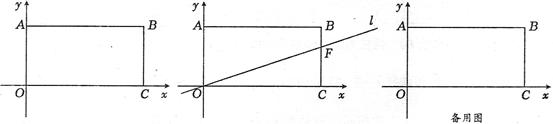
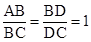 ,求
,求 的值;
的值;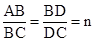 ,请探究并直接写出
,请探究并直接写出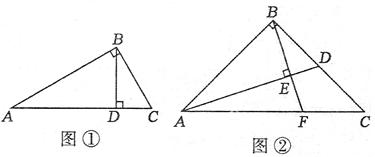
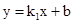 的图象过点A(0,3),且与反比例函数
的图象过点A(0,3),且与反比例函数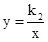
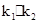 的值;
的值;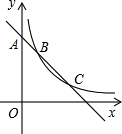
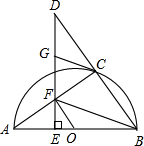
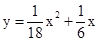
 .发射3 s后,导弹到达A点,此时位于与L同一水平面的R处雷达站测得AR的距离是2 km,再过3s后,导弹到达B点.
.发射3 s后,导弹到达A点,此时位于与L同一水平面的R处雷达站测得AR的距离是2 km,再过3s后,导弹到达B点.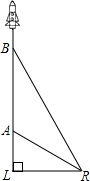
 粤公网安备 44130202000953号
粤公网安备 44130202000953号