现有编号分别为1，2，3，4，5，6，7， 8，9的九道不同的数学题。某同学从这九道题中一次随机抽取两道题，每题被抽到的概率是相等的，用符号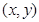
表示事件“抽到两 题的编号分别为
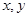,且
＜
”.
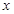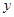（1）共有多少个基本事件？并列举出来；
（2）求该同学所抽取的两道题的编号之和小于17但不小于11的概率.
.
个学生参加考试（
），被抽过的考签立刻放回，求在考试结束之后，至少有一张考签没有被抽到的概率.
中，
，则
的值为多少？
.推荐套卷
现有编号分别为1，2，3，4，5，6，7， 8，9的九道不同的数学题。某同学从这九道题中一次随机抽取两道题，每题被抽到的概率是相等的，用符号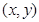表示事件“抽到两 题的编号分别为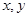,且＜”.
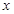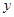（1）共有多少个基本事件？并列举出来；
（2）求该同学所抽取的两道题的编号之和小于17但不小于11的概率.
粤公网安备 44130202000953号