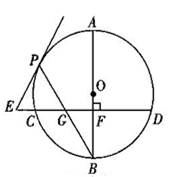
如图，已知AB是⊙O的直径，BP是⊙O的弦，弦CD⊥AB于点F，交BP于点G，E在CD的延长线上，EP=EG,
（1）求证：直线EP为⊙O的切线；
（2）点P在劣弧AC上运动，其他条件不变，若BG²=BF·BO.试证明BG=PG.
（3）在满足（2）的条件下，已知⊙O的半径为3，sinB=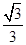
.求弦CD的长.
，求a2+b2的平方根。
，其中
－
︱+︱
相关知识点
推荐套卷
如图，已知AB是⊙O的直径，BP是⊙O的弦，弦CD⊥AB于点F，交BP于点G，E在CD的延长线上，EP=EG,
（1）求证：直线EP为⊙O的切线；
（2）点P在劣弧AC上运动，其他条件不变，若BG²=BF·BO.试证明BG=PG.
（3）在满足（2）的条件下，已知⊙O的半径为3，sinB=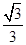.求弦CD的长.
粤公网安备 44130202000953号