第十五届中国“西博会”将于2014年10月底在成都召开,现有20名志愿者准备参加某分会场的工作,其中男生8人,女生12人.
(1)若从这20人中随机选取一人作为联络员,求选到女生的概率;
(2)若该分会场的某项工作只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁参加,游戏规则如下:将四张牌面数字分别为2、3、4、5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲参加,否则乙参加.试问这个游戏公平吗?请用树状图或列表法说明理由.
相关知识点
推荐套卷
 交AC于点E,F是
交AC于点E,F是
 ,AE=
,AE= ,求sin∠AFE的值和AF的长.
,求sin∠AFE的值和AF的长.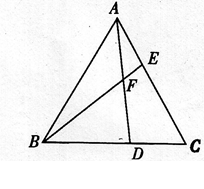
 ≌△CAD;
≌△CAD; 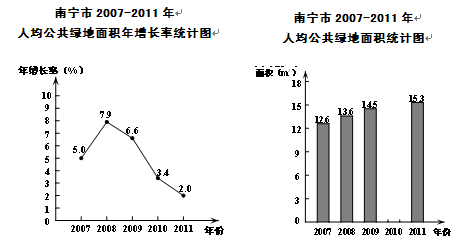
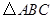 和点
和点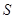 在平面直角坐标系中的位置如图所示:
在平面直角坐标系中的位置如图所示: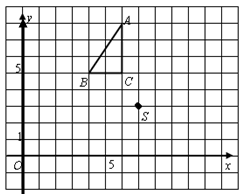
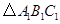 ,则点
,则点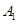 的坐标是,点
的坐标是,点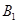 的坐标是 ;
的坐标是 ;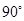 ,画出旋转后的图形.
,画出旋转后的图形. 粤公网安备 44130202000953号
粤公网安备 44130202000953号