如图，等边三角形OAB的边长为8
，且其三个顶点均在抛物线E：x2＝2py(p>0)上．
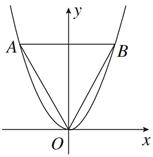
(1)求抛物线E的方程；
(2)设动直线l与抛物线E相切于点P，与直线y＝－1相交于点Q，证明以PQ为直径的圆恒过y轴上某定点．
，
的最小正周期；
，求
的最大值和最小值．
在
上是偶函数，在区间
上递增，且有
，求
的取值范围．
的值域．
，求证
．相关知识点
推荐套卷
如图，等边三角形OAB的边长为8，且其三个顶点均在抛物线E：x2＝2py(p>0)上．
(1)求抛物线E的方程；
(2)设动直线l与抛物线E相切于点P，与直线y＝－1相交于点Q，证明以PQ为直径的圆恒过y轴上某定点．
粤公网安备 44130202000953号