已知椭圆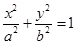
 的左、右焦点分别是
的左、右焦点分别是 、
、 ,
, 是椭圆右准线上的一点,线段
是椭圆右准线上的一点,线段 的垂直平分线过点
的垂直平分线过点 .又直线
.又直线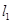 :
: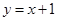 按向量
按向量 平移后的直线是
平移后的直线是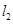 ,直线
,直线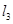 :
: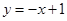 按向量
按向量 平移后的直线是
平移后的直线是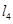 (其中
(其中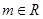 ).
).
(1)求椭圆的离心率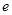 的取值范围.
的取值范围.
(2)当离心率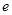 最小且
最小且 时,求椭圆的方程.
时,求椭圆的方程.
(3)若直线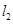 与
与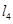 相交于(2)中所求得的椭圆内的一点
相交于(2)中所求得的椭圆内的一点 ,且
,且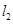 与这个椭圆交于
与这个椭圆交于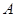 、
、 两点,
两点,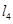 与这个椭圆交于
与这个椭圆交于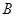 、
、 两点.求四边形ABCD面积
两点.求四边形ABCD面积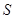 的取值范围.
的取值范围.
推荐套卷
已知椭圆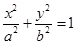
 的左、右焦点分别是
的左、右焦点分别是 、
、 ,
, 是椭圆右准线上的一点,线段
是椭圆右准线上的一点,线段 的垂直平分线过点
的垂直平分线过点 .又直线
.又直线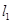 :
: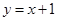 按向量
按向量 平移后的直线是
平移后的直线是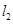 ,直线
,直线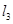 :
: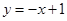 按向量
按向量 平移后的直线是
平移后的直线是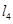 (其中
(其中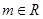 ).
).
(1)求椭圆的离心率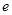 的取值范围.
的取值范围.
(2)当离心率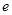 最小且
最小且 时,求椭圆的方程.
时,求椭圆的方程.
(3)若直线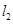 与
与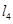 相交于(2)中所求得的椭圆内的一点
相交于(2)中所求得的椭圆内的一点 ,且
,且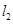 与这个椭圆交于
与这个椭圆交于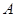 、
、 两点,
两点,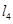 与这个椭圆交于
与这个椭圆交于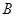 、
、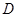 两点.求四边形ABCD面积
两点.求四边形ABCD面积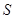 的取值范围.
的取值范围.