已知函数 的反函数为
的反函数为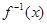 ,设
,设 的图象上在点
的图象上在点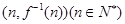 处的切线在y轴上的截距为
处的切线在y轴上的截距为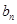 ,数列{
,数列{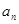 }满足:
}满足: .(1)求数列{
.(1)求数列{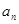 }的通项公式;
}的通项公式;
(2)在数列 中,仅
中,仅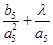 最小,求
最小,求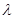 的取值范围;
的取值范围;
(3)令函数 数列
数列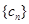 满足
满足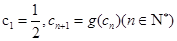 ,求证:对一切n≥2的正整数都有
,求证:对一切n≥2的正整数都有 .
.
推荐套卷
已知函数 的反函数为
的反函数为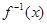 ,设
,设 的图象上在点
的图象上在点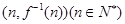 处的切线在y轴上的截距为
处的切线在y轴上的截距为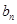 ,数列{
,数列{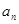 }满足:
}满足: .(1)求数列{
.(1)求数列{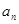 }的通项公式;
}的通项公式;
(2)在数列 中,仅
中,仅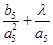 最小,求
最小,求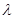 的取值范围;
的取值范围;
(3)令函数 数列
数列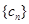 满足
满足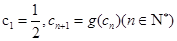 ,求证:对一切n≥2的正整数都有
,求证:对一切n≥2的正整数都有 .
.