设二次函数f(x)＝ax2＋bx＋c，函数F(x)＝f(x)－x的两个零点为m，n(m<n)．
(1)若m＝－1，n＝2，求不等式F(x)>0的解集；
(2)若a>0，且0<x<m<n<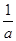
，比较f(x)与m的大小．
相关试题
的前n项和为Sn，且满足
中，A、B、C的对边分别是a、b、c，且A、B、C成等差数列．
． 
，求:a,c的值．
前
项和
.
,求
的值.相关知识点
推荐套卷
设二次函数f(x)＝ax2＋bx＋c，函数F(x)＝f(x)－x的两个零点为m，n(m<n)．
(1)若m＝－1，n＝2，求不等式F(x)>0的解集；
(2)若a>0，且0<x<m<n<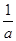，比较f(x)与m的大小．
粤公网安备 44130202000953号