如图,设有双曲线 ,F1,F2是其两个焦点,点M在双曲线上.
,F1,F2是其两个焦点,点M在双曲线上.
(1)若∠F1MF2=90°,求△F1MF2的面积;
(2)若∠F1MF2=60°,△F1MF2的面积是多少?若∠F1MF2=120°,△F1MF2的面积又是多少?
(3)观察以上计算结果,你能看出随∠F1MF2的变化,△F1MF2的面积将怎样变化吗?试证明你的结论.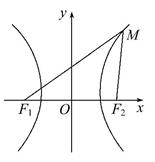
相关知识点
推荐套卷
如图,设有双曲线 ,F1,F2是其两个焦点,点M在双曲线上.
,F1,F2是其两个焦点,点M在双曲线上.
(1)若∠F1MF2=90°,求△F1MF2的面积;
(2)若∠F1MF2=60°,△F1MF2的面积是多少?若∠F1MF2=120°,△F1MF2的面积又是多少?
(3)观察以上计算结果,你能看出随∠F1MF2的变化,△F1MF2的面积将怎样变化吗?试证明你的结论.