提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:辆/千米)的函数.当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当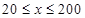 时,车流速度
时,车流速度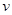 是车流密度x的一次函数.
是车流密度x的一次函数.
(Ⅰ)当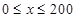 时,求函数
时,求函数 的表达式;
的表达式;
(Ⅱ)当车流密度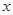 为多大时,车流量(单位时间内通过桥上某观察点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观察点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).
推荐套卷
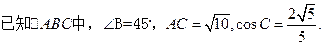
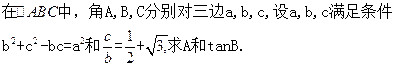
 的左、右焦点分别为
的左、右焦点分别为 ,
, ,过
,过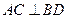 ,垂足为P.
,垂足为P.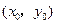 ,证明:
,证明: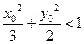 ;
; 与直线
与直线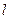 :x + y = 1相交于两个不同的点A、B.
:x + y = 1相交于两个不同的点A、B.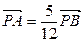 ,求
,求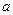 的值
的值 代表实数,讨论方程
代表实数,讨论方程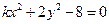 所表示的曲线。
所表示的曲线。 粤公网安备 44130202000953号
粤公网安备 44130202000953号