如图，单位圆(半径为1的圆)的圆心O为坐标原点，单位圆与y轴的正半轴交于点A，与钝角α的终边OB交于点B(xB，yB)，设∠BAO＝β.
(1)用β表示α；
(2)如果 sin β＝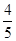
，求点B(xB，yB)坐标；
(3)求xB－yB的最小值．
，
，
．
能构成三角形，求实数
应满足的条件；
为直角三角形，且
为直角，求实数
，
．
及
的值；
的锐角
．
中，
，求
的值。
＝（2cos θ，2sin θ），向量
＝（
，－1），则|2
，试求
的值．相关知识点
推荐套卷
如图，单位圆(半径为1的圆)的圆心O为坐标原点，单位圆与y轴的正半轴交于点A，与钝角α的终边OB交于点B(xB，yB)，设∠BAO＝β.
(1)用β表示α；
(2)如果 sin β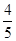＝，求点B(xB，yB)坐标；
(3)求xB－yB的最小值．
粤公网安备 44130202000953号