已知函数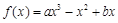 (
(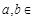 R),
R),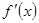 为其导函数,且
为其导函数,且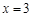 时
时 有极小值
有极小值 .
.
(1)求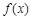 的单调递减区间;
的单调递减区间;
(2)若 ,
, ,当
,当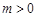 时,对于任意x,
时,对于任意x, 和
和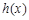 的值至少有一个是正数,求实数m的取值范围;
的值至少有一个是正数,求实数m的取值范围;
(3)若不等式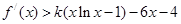 (
(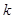 为正整数)对任意正实数
为正整数)对任意正实数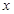 恒成立,求
恒成立,求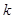 的最大值.
的最大值.
推荐套卷
已知函数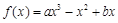 (
(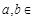 R),
R),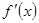 为其导函数,且
为其导函数,且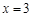 时
时 有极小值
有极小值 .
.
(1)求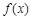 的单调递减区间;
的单调递减区间;
(2)若 ,
, ,当
,当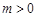 时,对于任意x,
时,对于任意x, 和
和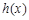 的值至少有一个是正数,求实数m的取值范围;
的值至少有一个是正数,求实数m的取值范围;
(3)若不等式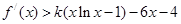 (
(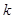 为正整数)对任意正实数
为正整数)对任意正实数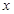 恒成立,求
恒成立,求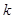 的最大值.
的最大值.