已知函数f(x)＝(x－a)(x－b)2，a，b是常数．
(1)若a≠b，求证：函数f(x)存在极大值和极小值；
(2)设(1)中f(x)取得极大值、极小值时自变量的值分别为x1，x2，设点A(x1，f(x1))，B(x2，f(x2))．如果直线AB的斜率为－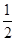
，求函数f(x)和f′(x)的公共递减区间的长度；
(3)若f(x)≥mxf′(x)对于一切x∈R恒成立，求实数m，a，b满足的条件．
相关试题
上任何一点
的切线与两坐标轴围成三角形面积是一个常数。
上有点
，用定义求：
处的切线的斜率；
上一点
的切线方程。
，
，其中
为常数。
在点
处的切线的斜率和切线方程；
的图象过点
的图象与
中切线的交点。
，求该物体在
时的瞬时速度；（2）已知
，求该物体在推荐套卷
已知函数f(x)＝(x－a)(x－b)2，a，b是常数．
(1)若a≠b，求证：函数f(x)存在极大值和极小值；
(2)设(1)中f(x)取得极大值、极小值时自变量的值分别为x1，x2，设点A(x1，f(x1))，B(x2，f(x2))．如果直线AB的斜率为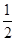－，求函数f(x)和f′(x)的公共递减区间的长度；
(3)若f(x)≥mxf′(x)对于一切x∈R恒成立，求实数m，a，b满足的条件．
粤公网安备 44130202000953号