如图，椭圆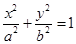
上的点M与椭圆右焦点
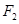的连线
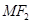与x轴垂直，且OM（O是坐标原点）与椭圆长轴和短轴端点的连线AB平行．
（1）求椭圆的离心率；
（2）F1是椭圆的左焦点，C是椭圆上的任一点，证明：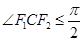
；
（3）过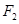且与AB垂直的直线交椭圆于P、Q，若
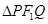的面积是20
，求此时椭圆的方程．
(
)
是△
的角平分线，∠
，
,求证
，直线
和曲线
有两个不同交点，它们围成区域为
,向
上随机投一点
，求
范围
+
+2=0的实根为
，方程
+
，试比较
的大小
=
+233，求
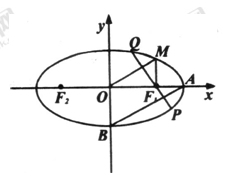
的值推荐套卷
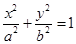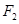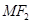如图，椭圆上的点M与椭圆右焦点的连线与x轴垂直，且OM（O是坐标原点）与椭圆长轴和短轴端点的连线AB平行．
（1）求椭圆的离心率；
（2）F1是椭圆的左焦点，C是椭圆上的任一点，证明：；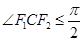
（3）过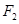且与AB垂直的直线交椭圆于P、Q，若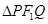的面积是20 ，求此时椭圆的方程．
粤公网安备 44130202000953号