在雅礼中学组织的“雅礼杯”篮球定点投篮比赛中，两人一对一比赛规则如下：若某人某次投篮命中，则由他继续投篮，否则由对方接替投篮. 现由甲、乙两人进行一对一投篮比赛，甲和乙每次投篮命中的概率分别是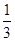
，
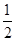.两人共投篮3次，且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.
（1）求3次投篮的人依次是甲、甲、乙的概率；
（2）若投篮命中一次得1分，否则得0分. 用ξ表示甲的总得分，求ξ的分布列和数学期望．
相关试题
，
为圆上任意一点，
的最值；（2）
的最值．
，
两点，且截
轴所得的弦长为
．求此圆的方程．
，
两点，且在两坐标轴上的四个截距之和为
的圆的方程．推荐套卷
在雅礼中学组织的“雅礼杯”篮球定点投篮比赛中，两人一对一比赛规则如下：若某人某次投篮命中，则由他继续投篮，否则由对方接替投篮. 现由甲、乙两人进行一对一投篮比赛，甲和乙每次投篮命中的概率分别是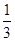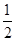，.两人共投篮3次，且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.
（1）求3次投篮的人依次是甲、甲、乙的概率；
（2）若投篮命中一次得1分，否则得0分. 用ξ表示甲的总得分，求ξ的分布列和数学期望．
粤公网安备 44130202000953号