如图，某大楼的顶部树有一块广告牌CD，小李在山坡的坡脚A处测得广告牌底部D的仰角为60°．沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°，已知山坡AB的坡度i=1：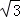
（i=1：
是指坡面的铅直高度BH与水平宽度AH的比），AB=10米，AE=15米．求广告牌CD的高度．
的解为正数。
。
是△ABC的三边，且满足
，判断△ABC的形状。
，把多项式
因式分解。
与
互为相反数，求方程
＝1的解。
，其中x满足
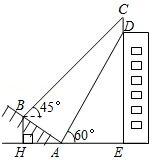
。相关知识点
推荐套卷
如图，某大楼的顶部树有一块广告牌CD，小李在山坡的坡脚A处测得广告牌底部D的仰角为60°．沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°，已知山坡AB的坡度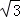i=1：（i=1：是指坡面的铅直高度BH与水平宽度AH的比），AB=10米，AE=15米．求广告牌CD的高度．
粤公网安备 44130202000953号