(本题满分14分)
如图1,直角梯形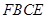 中, 四边形
中, 四边形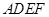 是正方形,
是正方形,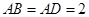 ,
, .将正方形沿
.将正方形沿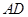 折起,得到如图2所示的多面体,其中面
折起,得到如图2所示的多面体,其中面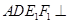 面
面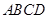 ,
,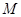 是
是 中点.
中点.
(1) 证明: ∥平面
∥平面 ;
;
(2) 求三棱锥 的体积.
的体积.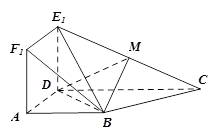
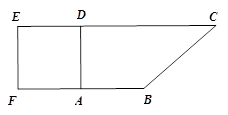
图1 图2
推荐套卷
(本题满分14分)
如图1,直角梯形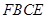 中, 四边形
中, 四边形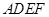 是正方形,
是正方形,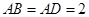 ,
, .将正方形沿
.将正方形沿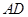 折起,得到如图2所示的多面体,其中面
折起,得到如图2所示的多面体,其中面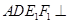 面
面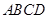 ,
,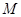 是
是 中点.
中点.
(1) 证明: ∥平面
∥平面 ;
;
(2) 求三棱锥 的体积.
的体积.

图1 图2