如图，
是抛物线为
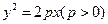上的一点，以S为圆心，r为半径（
）做圆，分别交x轴于A，B两点，连结并延长SA、SB，分别交抛物线于C、D两点。
（1）求证：直线CD的斜率为定值；
（2）延长DC交x轴负半轴于点E，若EC : ED =" 1" : 3，求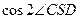
的值。
相关试题
的顶点
，顶点
在直线
上；
求点
，且
，求角
，其中
.
，求
在
的最小值；
在定义域内既有极大值又有极小值，求实数
的取值范围；
，使得当
时，不等式
恒成立.
中
，
为线段
上一点，且
，线段
．
，
，试求线段
的长.
的定义域为
，且同时满足以下三个条件：①
；②对任意的
，都有
；③当
时总有
．
的值；
时，恒有
．
千件，需另投入成本为
，当年产量不足80千件时，
（万元）.当年产量不小于80千件时，
（万元）.每件商品售价为500元.通过市场分析，该厂生产的商品能全部售完.
（万元）关于年产量相关知识点
推荐套卷
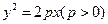如图，是抛物线为上的一点，以S为圆心，r为半径（）做圆，分别交x轴于A，B两点，连结并延长SA、SB，分别交抛物线于C、D两点。
（1）求证：直线CD的斜率为定值；
（2）延长DC交x轴负半轴于点E，若EC : ED =" 1" : 3，求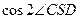的值。
粤公网安备 44130202000953号