如图，椭圆的中心为原点O，离心率e=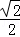
，一条准线的方程为x=2
．
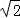（1）求该椭圆的标准方程．
（2）设动点P满足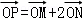
，其中M，N是椭圆上的点．直线OM与ON的斜率之积为﹣
．
问：是否存在两个定点F1，F2，使得|PF1|+|PF2|为定值．若存在，求F1，F2的坐标；若不存在，说明理由．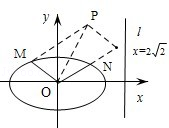
相关试题
.
，求曲线
在
处切线的斜率；
的单调区间；
，若对任意
，均存在
，使得 
，求
的取值范围.
在
及
时取得极值．
，都有
成立，求c的取值范围．
在
上是增函数；
在
上的值域。
的值；⑵判断
的奇偶性。
｝, B="{x|" 
} ，求：
⑵
。推荐套卷
如图，椭圆的中心为原点O，离心率e=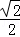，一条准线的方程为x=2．
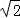（1）求该椭圆的标准方程．
（2）设动点P满足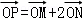，其中M，N是椭圆上的点．直线OM与ON的斜率之积为﹣．
问：是否存在两个定点F1，F2，使得|PF1|+|PF2|为定值．若存在，求F1，F2的坐标；若不存在，说明理由．
粤公网安备 44130202000953号