如图，把边长为10的正六边形纸板剪去相同的六个角，做成一个底面为正六边形的无盖六棱柱盒子，设其高为h，体积为V（不计接缝）.
（1）求出体积V与高h的函数关系式并指出其定义域；
（2）问当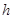
为多少时，体积V最大？最大值是多少？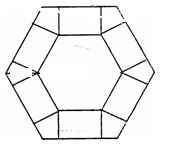
的终边上的点
与
关于
轴对称
，角
的终边上的点
与
关于直线
对称，求
之值．
，求
．
，且α∈(
，
)，求cosα，sinα的值．
，
，求
、
的范围。相关知识点
推荐套卷
如图，把边长为10的正六边形纸板剪去相同的六个角，做成一个底面为正六边形的无盖六棱柱盒子，设其高为h，体积为V（不计接缝）.
（1）求出体积V与高h的函数关系式并指出其定义域；
（2）问当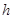为多少时，体积V最大？最大值是多少？
粤公网安备 44130202000953号