如图,已知双曲线C1: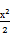 -y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.
-y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.
(1)在正确证明C1的左焦点是“C1-C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证).
(2)设直线y=kx与C2有公共点,求证|k|>1,进而证明原点不是“C1-C2型点”.
(3)求证:圆x2+y2= 内的点都不是“C1-C2型点”.
内的点都不是“C1-C2型点”.
相关知识点
推荐套卷
如图,已知双曲线C1: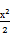 -y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.
-y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.
(1)在正确证明C1的左焦点是“C1-C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证).
(2)设直线y=kx与C2有公共点,求证|k|>1,进而证明原点不是“C1-C2型点”.
(3)求证:圆x2+y2= 内的点都不是“C1-C2型点”.
内的点都不是“C1-C2型点”.