已知点P是圆M:x2+(y+m)2=8(m>0,m≠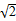 )上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.
)上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.
(1)当P在圆M上运动时,记动点Q的轨迹为曲线Г,判断曲线Г为何种曲线,并求出它的标准方程.
(2)过原点斜率为k的直线交曲线Г于A,B两点,其中A在第一象限,且它在x轴上的射影为点C,直线BC交曲线Г于另一点D,记直线AD的斜率为k′,是否存在m,使得对任意的k>0,都有|k·k′|=1?若存在,求m的值;若不存在,请说明理由.
相关知识点
推荐套卷
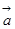 +
+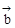 =
= ,
, ,求
,求 及
及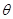 的余弦值.
的余弦值. .
.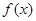 的极值;
的极值;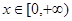 ,都有
,都有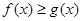 ,求实数a的取值范围.
,求实数a的取值范围.
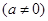 为奇函数,其图象在点
为奇函数,其图象在点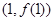 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数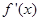 的最小值为
的最小值为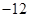 .
. ,
, ,
,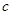 的值;
的值; 的单调递增区间,并求函数
的单调递增区间,并求函数 上的最大值和最小值.
上的最大值和最小值. 的正方形,且PD=
的正方形,且PD= .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号