在直角坐标平面上给定一曲线y2=2x,
(1)设点A的坐标为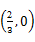
,求曲线上距点A最近的点P的坐标及相应的距离|PA|.
(2)设点A的坐标为(a,0),a∈R,求曲线上的点到点A距离的最小值dmin,并写出dmin=f(a)的函数表达式.
相关试题
的中心在坐标原点，焦点在
轴上且过点
，离心率是
．
的标准方程；
且与椭圆
，
两点，若
，求直线的方程.
，且
，求证：
、
（
）连线的斜率之积等于非零常数m的点的轨迹，加上
、
两点所成的曲线C可以是圆、椭圆或双曲线．求曲线C的方程，并讨论C的形状与m值得关系．
；
，若
是
的必
的取值范围．
，向量
，经过定点
以
为方向向量的直线与经过定点
以
为方向向量的直线相交于
，其中
，
的方程；（2）若
，过
的直线交曲线
两点，求
的取值范围。相关知识点
推荐套卷
在直角坐标平面上给定一曲线y2=2x,
(1)设点A的坐标为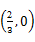,求曲线上距点A最近的点P的坐标及相应的距离|PA|.
(2)设点A的坐标为(a,0),a∈R,求曲线上的点到点A距离的最小值dmin,并写出dmin=f(a)的函数表达式.
粤公网安备 44130202000953号