已知函数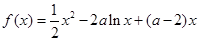 
，
．
(1）当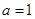 
时，求函数 
的最小值；
(2）当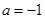
时，求证：无论
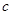取何值，直线
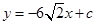均不可能与函数相切；
(3）是否存在实数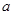
，对任意的 
，且
，有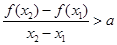
恒成立，若存在求出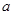的取值范围，若不存在，说明理由。
相关试题
，该动点的轨迹为F，
的最小值。
＝(cos
x，sin
＝(
)，且x∈[0，
]．
；
+
，求函数
的最值及相应的
的值。
满足：
，（n=1，2，…）。
，（n=1，2，…）。求数列
的通项公式；（2）求数列
的前n项和Sn。推荐套卷
已知函数 ，．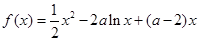
(1）当 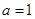时，求函数 的最小值；
(2）当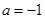 时，求证：无论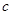取何值，直线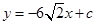均不可能与函数相切；
(3）是否存在实数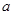，对任意的 ，且，有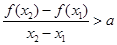恒成立，若存在求出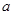的取值范围，若不存在，说明理由。
粤公网安备 44130202000953号