假设某班级教室共有4扇窗户，在每天上午第三节课上课预备铃声响起时，每扇窗户或被敞开或被关闭，且概率均为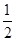
，记此时教室里敞开的窗户个数为X．
(1)求X的分布及数学期望；
(2)若此时教室里有两扇或两扇以上的窗户被关闭，班长就会将关闭的窗户全部敞开，否则维持原状不变．记每天上午第三节课上课时该教室里敞开的窗户个数为Y，求Y的数学期望．
,
,
,
,求
的取值范围。
，
，
，若
，
的值。
，
，
,求
的取值范围。相关知识点
推荐套卷
假设某班级教室共有4扇窗户，在每天上午第三节课上课预备铃声响起时，每扇窗户或被敞开或被关闭，且概率均为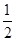，记此时教室里敞开的窗户个数为X．
(1)求X的分布及数学期望；
(2)若此时教室里有两扇或两扇以上的窗户被关闭，班长就会将关闭的窗户全部敞开，否则维持原状不变．记每天上午第三节课上课时该教室里敞开的窗户个数为Y，求Y的数学期望．
粤公网安备 44130202000953号