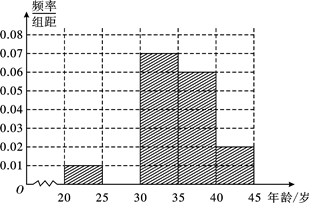
(本小题满分13分)为增强市民交通规范意识,我市面向全市征召劝导员志愿者,分布于各候车亭或十字路口处.现从符合条件的500名志愿者中随机抽取100名志愿者,他们的年龄情况如下表所示.
(1)频率分布表中的①、②位置应填什么数据?并在答题卡中补全频率分布直方图(如图),再根据频率分布直方图估计这500名志愿者中年龄在[30,35)岁的人数;
(2)在抽出的100名志愿者中按年龄再采用分层抽样法抽取20人参加“规范摩的司机的交通意识”培训活动,从这20人中选取2名志愿者担任主要负责人,记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学期望.
分组(单位:岁)
|
频数
|
频率
|
[20,25)
|
5
|
0.05
|
[25,30)
|
①
|
0.20
|
[30,35)
|
35
|
②
|
[35,40)
|
30
|
0.30
|
[40,45]
|
10
|
0.10
|
合计
|
100
|
1.00
|