如图,椭圆的离心率为,轴被曲线截得的线段长等于的长半轴长。

(1)求,的方程;
(2)设与轴的交点为,过坐标原点的直线与相交于点,直线分别与相交与.
①证明:;
②记的面积分别是.问:是否存在直线,使得=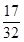 ?请说明理由。
?请说明理由。
推荐套卷
如图,椭圆的离心率为,轴被曲线截得的线段长等于的长半轴长。

(1)求,的方程;
(2)设与轴的交点为,过坐标原点的直线与相交于点,直线分别与相交与.
①证明:;
②记的面积分别是.问:是否存在直线,使得=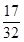 ?请说明理由。
?请说明理由。