在等腰直角△ABC中,∠BAC=90°,AB=AC,
(1)如图1,点D、E分别是AB、AC边的中点,AF⊥BE交BC于点F,连结EF、CD交于点H.求证,EF⊥CD;
(2)如图2,AD=AE,AF⊥BE于点G交BC于点F,过F作FP⊥CD交BE的延长线于点P,试探究线段BP,FP,AF之间的数量关系,并说明理由.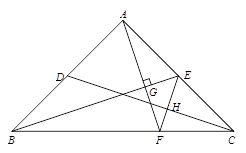
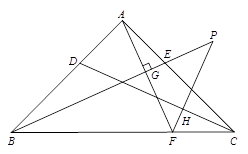
图1 图2
相关知识点
推荐套卷
在等腰直角△ABC中,∠BAC=90°,AB=AC,
(1)如图1,点D、E分别是AB、AC边的中点,AF⊥BE交BC于点F,连结EF、CD交于点H.求证,EF⊥CD;
(2)如图2,AD=AE,AF⊥BE于点G交BC于点F,过F作FP⊥CD交BE的延长线于点P,试探究线段BP,FP,AF之间的数量关系,并说明理由.

图1 图2