在平面直角坐标系中，曲线C1的参数方程为
（a＞b＞0，
为参数），以Ο为极点，x轴的正半轴为极轴建立极坐标系，曲线C2是圆心在极轴上且经过极点的圆，已知曲线C1上的点M
对应的参数=
，
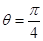与曲线C2交于点D
（1）求曲线C1，C2的方程；
（2）A（ρ1，θ），Β（ρ2，θ+
）是曲线C1上的两点，求
的值。
相关试题
且
,
的表达式； (2)判断
时，
恒成立，求
的取值范围.
，若存在
，使得
成立，则称
为
，若
内存在“滞点”，求
的取值范围.
，满足
的值； 
.
有两个实根
、
，且
．定义函数
．
的值；
在区间
上的单调性，并加以证明；
为正实数，证明不等式：
．相关知识点
推荐套卷
在平面直角坐标系中，曲线C1的参数方程为 （a＞b＞0，为参数），以Ο为极点，x轴的正半轴为极轴建立极坐标系，曲线C2是圆心在极轴上且经过极点的圆，已知曲线C1上的点M 对应的参数= 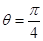，与曲线C2交于点D
（1）求曲线C1，C2的方程；
（2）A（ρ1，θ），Β（ρ2，θ+）是曲线C1上的两点，求的值。
粤公网安备 44130202000953号