(本小题满分14分)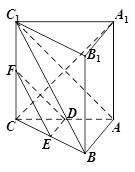
如图,在三棱柱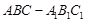 中,
中, 底面
底面 ,
,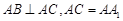 ,E、F分别是棱
,E、F分别是棱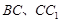 的中点.
的中点.
(1)求证:AB⊥平面AA1 C1C;
(2)若线段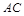 上的点
上的点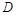 满足平面
满足平面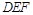 //平面
//平面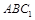 ,试确定点
,试确定点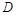 的位置,并说明理由;
的位置,并说明理由;
(3)证明: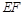 ⊥A1C.
⊥A1C.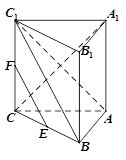
推荐套卷
(本小题满分14分)
如图,在三棱柱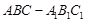 中,
中, 底面
底面 ,
,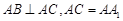 ,E、F分别是棱
,E、F分别是棱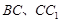 的中点.
的中点.
(1)求证:AB⊥平面AA1 C1C;
(2)若线段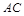 上的点
上的点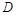 满足平面
满足平面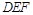 //平面
//平面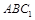 ,试确定点
,试确定点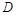 的位置,并说明理由;
的位置,并说明理由;
(3)证明: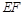 ⊥A1C.
⊥A1C.