在平面直角坐标系中,将坐标为(0,0),(2,4),(2,0),(4,4)的点用线段依次连接起来形成一个图案:
(1)若这四个点的纵坐标若保持不变,横坐标变为原来的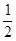 ,所得图案与原来的图案相比有什么变化?
,所得图案与原来的图案相比有什么变化?
(2)横坐标不变,纵坐标分别减3,所得图案与原来图案相比有什么变化?
(3)横坐标、纵坐标分别变为原来的2倍,所得图形与原图形相比有什么变化?
相关知识点
推荐套卷
在平面直角坐标系中,将坐标为(0,0),(2,4),(2,0),(4,4)的点用线段依次连接起来形成一个图案:
(1)若这四个点的纵坐标若保持不变,横坐标变为原来的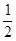 ,所得图案与原来的图案相比有什么变化?
,所得图案与原来的图案相比有什么变化?
(2)横坐标不变,纵坐标分别减3,所得图案与原来图案相比有什么变化?
(3)横坐标、纵坐标分别变为原来的2倍,所得图形与原图形相比有什么变化?