已知函数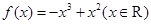 ,
, 满足
满足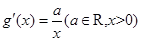 ,且
,且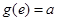 ,
,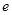 为自然对数的底数.
为自然对数的底数.
(1)已知 ,求
,求 在
在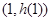 处的切线方程;
处的切线方程;
(2)若存在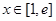 ,使得
,使得
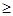
 成立,求
成立,求 的取值范围;
的取值范围;
(3)设函数 ,
,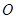 为坐标原点,若对于
为坐标原点,若对于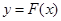 在
在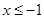 时的图象上的任一点
时的图象上的任一点 ,在曲线
,在曲线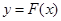
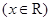 上总存在一点
上总存在一点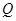 ,使得
,使得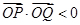 ,且
,且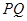 的中点在
的中点在 轴上,求
轴上,求 的取值范围.
的取值范围.
推荐套卷
已知函数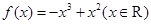 ,
, 满足
满足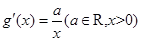 ,且
,且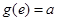 ,
,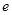 为自然对数的底数.
为自然对数的底数.
(1)已知 ,求
,求 在
在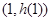 处的切线方程;
处的切线方程;
(2)若存在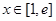 ,使得
,使得
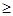
 成立,求
成立,求 的取值范围;
的取值范围;
(3)设函数 ,
,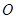 为坐标原点,若对于
为坐标原点,若对于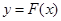 在
在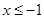 时的图象上的任一点
时的图象上的任一点 ,在曲线
,在曲线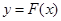
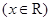 上总存在一点
上总存在一点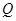 ,使得
,使得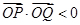 ,且
,且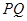 的中点在
的中点在 轴上,求
轴上,求 的取值范围.
的取值范围.