某大型公益活动从一所名牌大学的四个学院中选出了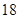
名学生作为志愿者，参加相关的活
动事宜．学生来源人数如下表：
| 学院 |
外语学院 |
生命科学学院 |
化工学院 |
艺术学院 |
| 人数 |
 |
 |
 |
 |
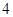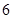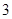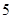（1）若从这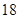名学生中随机选出两名，求两名学生来自同一学院的概率；
（2）现要从这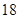名学生中随机选出两名学生向观众宣讲此次公益活动的主题．设其中来自外语学院的人数为
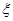，令
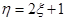，求随机变量
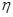的分布列及数学期望
.
（
），
，当
取何值时，（1）
；（2）
分别取什么值时，复数
是（1）实数（2）虚数（3）纯虚数。
的方程
有实根，求实数
的取值。
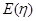是纯虚数；推荐套卷
某大型公益活动从一所名牌大学的四个学院中选出了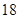名学生作为志愿者，参加相关的活
动事宜．学生来源人数如下表：
| 学院 |
外语学院 |
生命科学学院 |
化工学院 |
艺术学院 |
| 人数 |
|
|
|
|
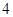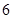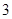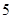（1）若从这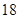名学生中随机选出两名，求两名学生来自同一学院的概率；
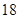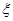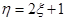（2）现要从这名学生中随机选出两名学生向观众宣讲此次公益活动的主题．设其中来自外语学院的人数为，令，求随机变量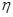的分布列及数学期望.
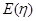粤公网安备 44130202000953号