如图,已知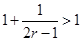 ,
, ,
, ,
,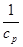 分别是椭圆
分别是椭圆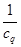 的四个顶点,△
的四个顶点,△ 是一个边长为2的等边三角形,其外接圆为圆
是一个边长为2的等边三角形,其外接圆为圆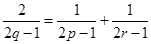 .
.
(1)求椭圆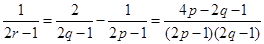 及圆
及圆 的方程;
的方程;
(2)若点 是圆
是圆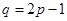 劣弧
劣弧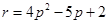 上一动点(点
上一动点(点 异于端点
异于端点 ,
, ),直线
),直线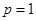 分别交线段
分别交线段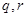 ,椭圆
,椭圆 于点
于点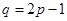 ,
,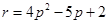 ,直线
,直线 与
与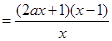 交于点
交于点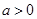 .
.
(ⅰ)求 的最大值;
的最大值;
(ⅱ)试问: ,
,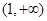 两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.
两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.
推荐套卷
如图,已知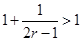 ,
, ,
, ,
,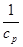 分别是椭圆
分别是椭圆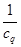 的四个顶点,△
的四个顶点,△ 是一个边长为2的等边三角形,其外接圆为圆
是一个边长为2的等边三角形,其外接圆为圆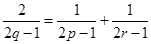 .
.
(1)求椭圆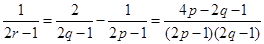 及圆
及圆 的方程;
的方程;
(2)若点 是圆
是圆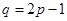 劣弧
劣弧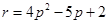 上一动点(点
上一动点(点 异于端点
异于端点 ,
, ),直线
),直线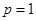 分别交线段
分别交线段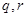 ,椭圆
,椭圆 于点
于点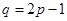 ,
,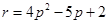 ,直线
,直线 与
与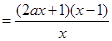 交于点
交于点 .
.
(ⅰ)求 的最大值;
的最大值;
(ⅱ)试问: ,
,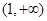 两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.
两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.