某种树苗栽种时高度为A(A为常数)米，栽种n年后的高度记为f(n)．经研究发现f(n)近似地满足 f(n)＝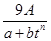
，其中
，a，b为常数，n∈N，f(0)＝A．已知栽种3年后该树木的高度为栽种时高度的3倍．
（1）栽种多少年后，该树木的高度是栽种时高度的8倍；
（2）该树木在栽种后哪一年的增长高度最大．
相关试题
，
，
．
能构成三角形，求实数
应满足的条件；
为直角三角形，且
为直角，求实数
，
．
及
的值；
的锐角
．
，且
均为钝角，求
的值．
．
=（x，3）．
，求x的值；
，求x的值．相关知识点
推荐套卷
某种树苗栽种时高度为A(A为常数)米，栽种n年后的高度记为f(n)．经研究发现f(n)近似地满足 f(n)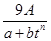＝，其中，a，b为常数，n∈N，f(0)＝A．已知栽种3年后该树木的高度为栽种时高度的3倍．
（1）栽种多少年后，该树木的高度是栽种时高度的8倍；
（2）该树木在栽种后哪一年的增长高度最大．
粤公网安备 44130202000953号