(本小题12分)已知某校高二文科班学生的化学与物理的水平测试成绩抽样统计如下表,若抽取学生n人,成绩分为A(优秀)、B(良好)、C(及格)三个等级,设x,y分别表示化学成绩与物理成绩.例如:表中化学成绩为B等级的共有20+18+4=42人,已知x与y均为B等级的概率是0.18.
x
人数
y
|
A
|
B
|
C
|
A
|
7
|
20
|
5
|
B
|
9
|
18
|
6
|
C
|
a
|
4
|
b
|
(1)求抽取的学生人数;
(2)设该样本中,化学成绩优秀率是30%,求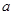 ,
,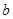 值;
值;
(3)在物理成绩为C等级的学生中,已知a≥10,b≥8,求化学成绩为A等级的人数比C等级的人数少的概率.