甲、乙两名运动员参加“选拔测试赛”,在相同条件下,两人5次测试的成绩(单位:分)记录如下:
甲 86 77 92 72 78
乙 78 82 88 82 95
(1)用茎叶图表示这两组数据;.
(2)现要从中选派一名运动员参加比赛,你认为选派谁参赛更好?说明理由(不用计算);
(3)若将频率视为概率,对运动员甲在今后三次测试成绩进行预测,记这三次成绩高于 分的次数为
分的次数为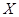 ,求
,求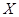 的分布列和数学期望
的分布列和数学期望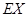 ..
..
相关知识点
推荐套卷
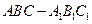 中, AB=1,
中, AB=1, ,∠ABC=60
,∠ABC=60 .
.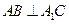 ;
; —B的余弦值。
—B的余弦值。
 等比数列
等比数列 的前
的前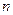 项和,且
项和,且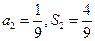
 数列
数列 ,求数列
,求数列 的前
的前 中,
中,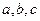 分别是角
分别是角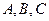 的对边,且有
的对边,且有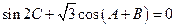 .若
.若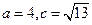 ,
,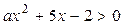 的解集是
的解集是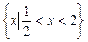 ,
, 的值; (2) 求不等式
的值; (2) 求不等式 的解集.
的解集.
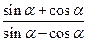 的值(2)求
的值(2)求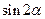 的值
的值 粤公网安备 44130202000953号
粤公网安备 44130202000953号