尔凡驾车从甲地到乙地,设他出发第xmin时的速度为ykm/h,图中的折线表示他在整个驾车过程中y与x之间的函数关系.
(1)当20≤x≤30时,汽车的平均速度为 km/h,该段时间行驶的路程为 km;
(2)当30≤x≤35时,求y与x之间的函数关系式,并求出尔凡出发第32min时的速度;
(3)如果汽车每行驶100km耗油8L,那么尔凡驾车从甲地到乙地共耗油多少升?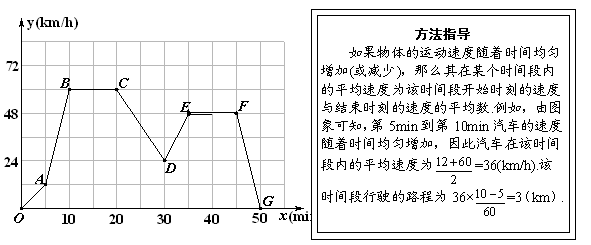
相关知识点
推荐套卷
尔凡驾车从甲地到乙地,设他出发第xmin时的速度为ykm/h,图中的折线表示他在整个驾车过程中y与x之间的函数关系.
(1)当20≤x≤30时,汽车的平均速度为 km/h,该段时间行驶的路程为 km;
(2)当30≤x≤35时,求y与x之间的函数关系式,并求出尔凡出发第32min时的速度;
(3)如果汽车每行驶100km耗油8L,那么尔凡驾车从甲地到乙地共耗油多少升?