如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=90°,且EF交正方形外角的平分线CF于点F.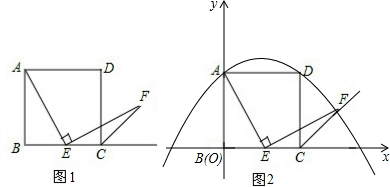
(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否总成立?请给出证明;
②在如图2的直角坐标系中,当点E滑动到某处时,点F恰好落在抛物线y=-x2+x+1上,求此时点F的坐标.
相关知识点
推荐套卷
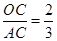 ,且OC=4,求PA的长和tanD的值.
,且OC=4,求PA的长和tanD的值.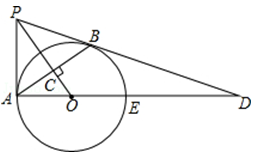
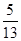 .求⊙O的半径.
.求⊙O的半径.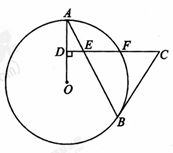
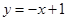 的图象上的概率;
的图象上的概率; 粤公网安备 44130202000953号
粤公网安备 44130202000953号