如图,在四棱锥P - ABCD中,平面PAD⊥平面ABCD,AB∥DC,
△PAD是等边三角形,已知BD ="2AD" =8,AB ="2DC" =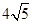 .
.
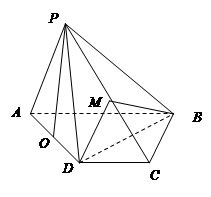
(I)设M是PC上的一点,证明:平面MBD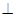 平面PAD;
平面PAD;
(Ⅱ)求三棱锥C—PAB的体积.
相关知识点
推荐套卷
如图,在四棱锥P - ABCD中,平面PAD⊥平面ABCD,AB∥DC,
△PAD是等边三角形,已知BD ="2AD" =8,AB ="2DC" =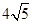 .
.

(I)设M是PC上的一点,证明:平面MBD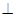 平面PAD;
平面PAD;
(Ⅱ)求三棱锥C—PAB的体积.