(本小题满分12分)
为了解大学生身体素质情况,从某大学共800名男生中随机抽取50人测量身高。 据测量,被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组:第一组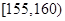 ;第二组
;第二组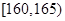 ;…;第八组
;…;第八组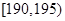 .如图是按上述分组方法得到的频率分布直方图.
.如图是按上述分组方法得到的频率分布直方图.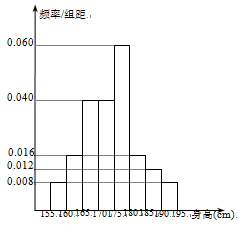
(1)估计这所学校高三年级全体男生身高在180cm以上(含180cm)的人数;
(2)若从身高属于第六组和第八组的所有男生中随机抽取两人,记他们的身高分别为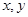 ,求满足“
,求满足“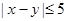 ”的事件的概率.
”的事件的概率.
推荐套卷
(本小题满分12分)
为了解大学生身体素质情况,从某大学共800名男生中随机抽取50人测量身高。 据测量,被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组:第一组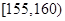 ;第二组
;第二组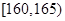 ;…;第八组
;…;第八组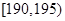 .如图是按上述分组方法得到的频率分布直方图.
.如图是按上述分组方法得到的频率分布直方图.
(1)估计这所学校高三年级全体男生身高在180cm以上(含180cm)的人数;
(2)若从身高属于第六组和第八组的所有男生中随机抽取两人,记他们的身高分别为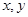 ,求满足“
,求满足“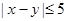 ”的事件的概率.
”的事件的概率.