（本小题满分13分）已知函数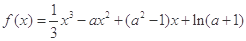
（其中
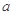为常数）.
（1）若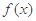
在区间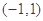
上不单调，求
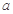的取值范围；
（2）记函数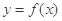
的极大值点为
，极小值点为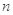
，若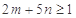
恒成立，试求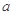的取值范围；
（3）若存在一条与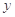
轴垂直的直线和函数
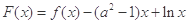的图象相切，且切点的横坐标
满足
，求实数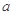的取值范围.
相关试题
，求
的值．
，
，若
，求
的解析式．
，试比较
与
的大小．
(a＞1).
，表示某一时刻一立方米湖水中所含污染物的克数（我们称其湖水污染质量分数），
表示湖水污染初始质量分数.
时，湖水的污染程度如何.推荐套卷
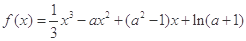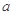（本小题满分13分）已知函数（其中为常数）.
（1）若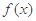在区间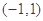上不单调，求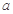的取值范围；
（2）记函数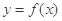的极大值点为，极小值点为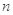，若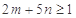恒成立，试求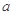的取值范围；
（3）若存在一条与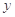轴垂直的直线和函数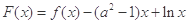的图象相切，且切点的横坐标满足，求实数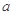的取值范围.
粤公网安备 44130202000953号