(本小题满分13分)
某旅游景区的观景台P位于高(山顶到山脚水平面M的垂直高度PO)为2km的山峰上,山脚下有一段位于水平线上笔直的公路AB,山坡面可近似地看作平面PAB,且△PAB为等腰三角形.山坡面与山脚所在水平面M所成的二面角为α(0°<α<90°),且sinα=.现从山脚的水平公路AB某处C0开始修建一条盘山公路,该公路的第一段、第二段、第三段…,第n-1段依次为C0C1,C1C2,C2C3,…,Cn-1Cn(如图所示),且C0C1,C1C2,C2C3,…,Cn-1Cn与AB所成的角均为β,其中0<β<90°,sinβ=.试问:
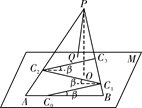
(1)每修建盘山公路多少米,垂直高度就能升高100米.若修建盘山公路至半山腰(高度为山高的一半),在半山腰的中心Q处修建上山缆车索道站,索道PQ依山而建(与山坡面平行,离坡面高度忽略不计),问盘山公路的长度和索道的长度各是多少?
(2)若修建xkm盘山公路,其造价为 a万元.修建索道的造价为2a万元/km.问修建盘山公路至多高时,再修建上山索道至观景台,总造价最少.