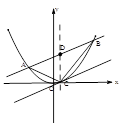
我们将不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点称为切点.解决下列问题:
已知抛物线
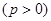 上的点
上的点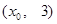 到焦点的距离等于4,直线
到焦点的距离等于4,直线 与抛物线相交于不同的两点
与抛物线相交于不同的两点 、
、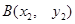 ,且
,且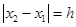 (
( 为定值).设线段
为定值).设线段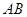 的中点为
的中点为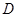 ,与直线
,与直线 平行的抛物线的切点为
平行的抛物线的切点为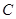 ..
..
(1)求出抛物线方程,并写出焦点坐标、准线方程;
(2)用 、
、 表示出
表示出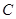 点、
点、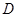 点的坐标,并证明
点的坐标,并证明 垂直于
垂直于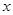 轴;
轴;
(3)求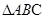 的面积,证明
的面积,证明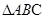 的面积与
的面积与 、
、 无关,只与
无关,只与 有关.
有关.
相关知识点
推荐套卷
 是一个等差数列,且
是一个等差数列,且 ,
, 。
。 ;
; 的最大值.
的最大值.
 ,求AB1与C1B所成角的大小。
,求AB1与C1B所成角的大小。
 的定义域为
的定义域为 ,且满足对于任意
,且满足对于任意 ,有
,有 .
. 的值;
的值; ≤
≤ ,且
,且 上是增函数,求
上是增函数,求 的取值范围.
的取值范围.
 的定义域和值域均是
的定义域和值域均是 ,求实数
,求实数 的值;
的值; 上是减函数,且对任意的
上是减函数,且对任意的 ,总有
,总有 ≤
≤ ,求实数
,求实数 粤公网安备 44130202000953号
粤公网安备 44130202000953号