如图,直线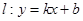 与抛物线
与抛物线 (常数
(常数 )相交于不同的两点
)相交于不同的两点 、
、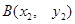 ,且
,且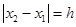 (
(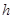 为定值),线段
为定值),线段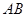 的中点为
的中点为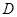 ,与直线
,与直线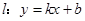 平行的切线的切点为
平行的切线的切点为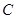 (不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(1)用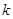 、
、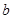 表示出
表示出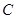 点、
点、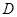 点的坐标,并证明
点的坐标,并证明 垂直于
垂直于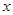 轴;
轴;
(2)求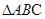 的面积,证明
的面积,证明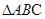 的面积与
的面积与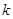 、
、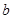 无关,只与
无关,只与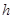 有关;
有关;
(3)小张所在的兴趣小组完成上面两个小题后,小张连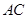 、
、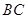 ,再作与
,再作与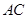 、
、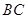 平行的切线,切点分别为
平行的切线,切点分别为 、
、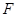 ,小张马上写出了
,小张马上写出了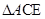 、
、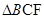 的面积,由此小张求出了直线
的面积,由此小张求出了直线 与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
相关知识点
推荐套卷
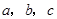 ,已知
,已知 ,
, .
.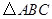 的面积等于
的面积等于 ,求
,求 ;
; ,求
,求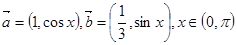 .
. ,求
,求 的值;
的值; ,求
,求 的值.
的值. 、
、 是不共线的两个非零向量.
是不共线的两个非零向量. ,求证:
,求证: 三点共线;
三点共线; 与
与 共线,求实数
共线,求实数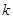 的值.
的值. .
.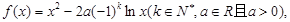
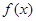 的单调性;
的单调性;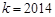 时,关于
时,关于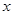 的方程
的方程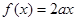 有唯一解,求
有唯一解,求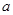 的值;
的值; 时,证明: 对一切
时,证明: 对一切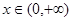 ,都有
,都有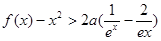 成立.
成立. 粤公网安备 44130202000953号
粤公网安备 44130202000953号